3. Расчет срока службы конструкции обуви в полупаре

Если в полупаре изнашивается одна деталь, то срок службы полупары обуви соответствует сроку службы этой детали. Однако обувь состоит из многих различных деталей и узлов, находящихся при эксплуатации в разных условиях и выходящих из строя неодновременно. При большом разнообразии деталей в обуви представляется возможным все дефекты свести к трем основным видам: дефекты, нарушающие целостность деталей верха А, деталей низа Б и дефекты системы скрепления деталей верха обуви с низом В. Выход обуви из строя может происходить по одному, двум или одновременно по дефектам всех трех видов. Используя правила перемножения вероятностей с выражением их через вероятности противоположных событий и учитывая, что вероятность появления бездефектных полупар равна произведению вероятностей появления бездефектных полупар по каждому из дефектов А, Б и В, показано, что вероятность дефектной обуви равна 1 - А*Б*В^*.

^* (Подробнее с этим методом можно ознакомиться в работе Черникова Н. Н. и Колесниковой А. И. "Метод установления износостойкости обуви". Научно-исследовательские труды ЦНИИКП, № 29, 1959.)

Расчет среднего срока службы конструкции обуви обычно производят графическим методом.

Исходными данными для расчета являются средние сроки службы отдельных деталей M и координаты начала лучей. На диаграмму наносят выравнивающие прямые сроков служб отдельных деталей в виде лучей, выходящих из точек (x_i*t_i = -2,5) и проходящих через соответствующие значения средних сроков службы деталей M.

Далее для детали с наименьшим сроком службы из точки на луче, соответствующей сроку службы этой детали, опускают перпендикуляр, пересекающий лучи, соответствующие остальным деталям. Для точек пересечения находят процент дефектных полупар с остальными дефектами на момент носки, соответствующий среднему сроку службы детали, имеющей наименьший срок службы M_min.

Вычитая из единицы величины, найденные для каждой детали, получают вероятности появления полупар без дефектов по каждой детали. Затем произведение полученных вероятностей уменьшают на 0,5 (так как вероятность появления бездефектной детали в момент M_min, соответствующий ее сроку службы, равна 0,5); результат дает вероятность наличия полупар без какого-либо дефекта P_{А, Б, В}:

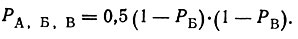
P_{А, Б, В} в численно равно доле бездефектных полупар, а (1 - P_{А, Б, В}) - доле полупар хотя бы с одним дефектом в момент M_min. На бумаге со шкалой вероятностей проводят луч из точки 0, соответствующей моменту появления дефектов наименее износостойкой детали (x_min, t = -2,5), в точку с координатами M_min и процент обуви хотя бы с одним из дефектов А, Б, В. Пересечение полученного луча с линией сроков службы даст точку M, соответствующую среднему сроку службы конструкции обуви.

Пример. При носке обуви была получена следующая характеристика износостойкости ее по началу появления дефектов отдельных элементов конструкции и средним сроком службы M в днях этих элементов:

Проводим лучи для каждого дефекта (рис. 242). Графическим путем устанавливаем количество полупар в момент M_min (230 дней). Количество полупар с дефектом А равно 30,2%, следовательно, количество обуви без дефектов верха равно 69,8%.

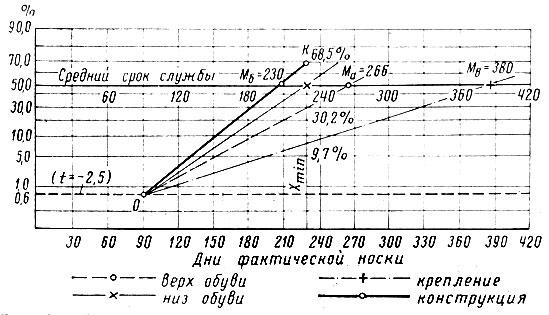
Рис. 242. График расчета среднего срока службы полупары обуви

Процент дефектов В за 230 дней носки и количество бездефектных по данному признаку полупар равно соответственно 9,7 и 90,3%. Общее количество бездефектных полупар за 230 дней носки равно 0,5×0,698×0,903×100=31,5%, а количество полупар, имеющих в конструкции дефекты А, Б и В, равно 68,5% (K). Из точки К проводим луч в точку начала появления дефектов x_i = 90, t = -2,5. Этот луч отсекает отрезок, соответствующий среднему сроку службы M конструкции обуви, равному 210 дням. Полученная величина срока службы является средним сроком службы полупары обуви.