Работа III.3. Определение связи между размерными признаками

Цель работы: научить студента пользоваться методами математической статистики при обработке результатов массового обмера.

Содержание работы.

1. Выбор интервала по каждому размерному признаку.

2. Составление корреляционной решетки.

3. Выбор рабочего начала и определение параметров решетки для подсчета моментов первой и второй степени.

4. Определение статистических параметров.

Пособия: карточки массового обмера с размерными признаками, бланки для составления корреляционных решеток и статистических вычислений.

Литература. Смирнов Н. В., Дунин-Барковский И. В. Краткий курс математической статистики для технических приложений, М., Физматиздат, 1959. Длин А. М. Математическая статистика в технике, М., "Советская наука", 1958.

Зыбин Ю. П. Конструирование изделий из кожи, М., "Легкая индустрия", 1968, стр. 72-80.

При массовом производстве обуви и перчаток необходимо знать, какие размеры стоп и кистей имеют люди, приобретающие эти изделия.

Для установления этих размеров производят массовые обмеры стоп и кистей. Данные массовых обмеров обрабатываются методами математической статистики для установления основных параметров, характеризующих группу людей по тем размерным признакам, которые были взяты в обследовании. Такими параметрами являются средние значения размерных признаков М_х, М_у и среднеквадратичные отклонения σ_х, σ_у. Кроме того, обработка данных обмера позволяет установить связь между двумя какими-либо размерными признаками (например, между длиной стопы Д и ее обхватом в плюсно-фаланговом сочленении О_0,68Д; между длиной стопы Д и шириной пятки Ш_п; между длиной кисти руки Д_к и длиной ее среднего пальца l₃ и т. п.).

Для установления такой связи прежде всего определяют коэффициент корреляции r, характеризующий тесноту связи между изучаемыми размерными признаками.

Если r = 0, то связи между изучаемыми явлениями не существует. При r = 1 связь является функциональной. Промежуточные значения 0 < r < 1 говорят о наличии связи более или менее сильной степени. Коэффициент корреляции может иметь положительный или отрицательный знак. Положительный знак говорит о прямой связи, отрицательный - об обратной. Если вслед за повышением величины одного признака увеличивается и второй признак, связь является прямой. При обратной связи увеличение значения одного признака вызывает уменьшение величины другого.

Считают обычно, что связь отсутствует, если r меньше 0,3; выражена умеренно, если r = 0,3÷0,5; значительна при r = 0,5÷0,7 и имеется тесная связь при r = 0,7÷0,9. Оценивая связь, следует учитывать число наблюдаемых случаев, так как при малом числе наблюдений в статистических показателях может быть большая ошибка.

1. Выбор интервала по каждому размерному признаку

Каждому студенту выдается 150-250 карточек, в которых записаны индивидуальные данные, полученные или по обмеру стопы, или по обмеру кисти. Например, одна из карточек по обмеру стопы содержит следующие данные, мм: 246 - длина стопы; 98 - ширина стопы по сечению 0,73Д, 240 - обхват по середине стопы; 338 - обхват через пятку-сгиб; 75 - ширина пятки в сечении 0,18Д.

Нужно установить связь между длиной стопы Д и ее шириной в сечении 0,73Д-Ш_0,73Д.

Прежде всего необходимо установить наибольшее и наименьшее значения длины стопы. Например, это будут величины 222 и 251 мм. Размах колебания признака составит 251 - 222 = 29 мм; эту величину необходимо разбить на 10-12 интервалов. Величину интервала d_x выбирают в зависимости от размаха колебания признака. В данном примере d_x = 3, т. е. получим 10 интервалов. Так же устанавливается интервал и для второго признака Ш_0,73Д. Он может отличаться от интервала для длины стопы.

2. Составление корреляционной решетки

В графы x и y разработочного бланка для антропометрических обмеров (табл. III.6) записывают максимальное, минимальное и среднее значения двух размерных признаков для каждого интервала. Из карточек, в которых записаны значения размерных признаков, надо установить частость распределения сочетаний двух выбранных размерных признаков, т. е. подсчитать, сколько раз при данном значении одного размерного признака встречается определенное значение второго (например, сколько раз при значении длины стопы в интервале 222-224 встречается значение обхвата стопы в интервале 80-82).

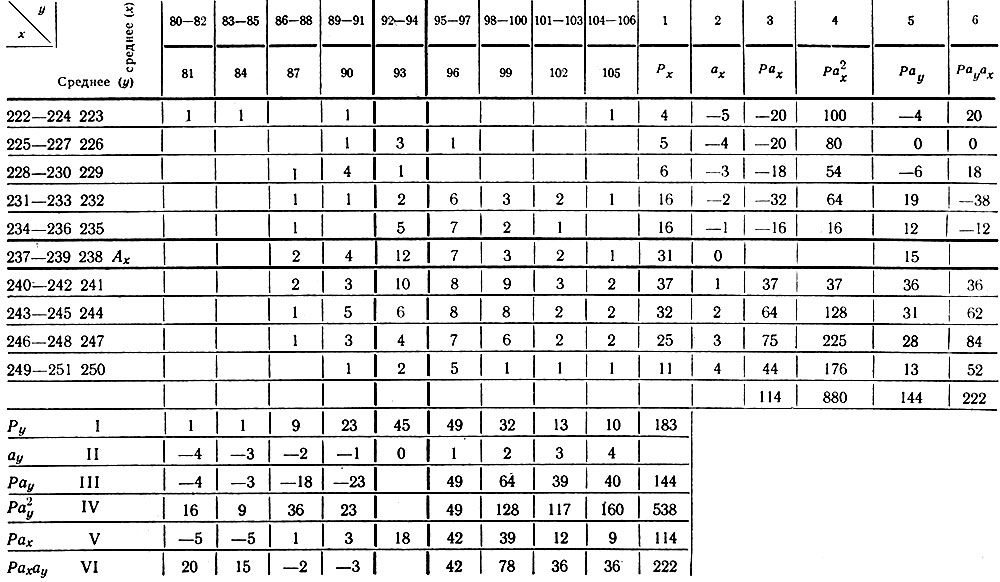
Таблица III.6. Разработочный бланк для антропометрических обмеров

Для удобства подсчета предлагается следующая условная запись. Вычерчивается решетка с ячейками размером 2×2 см. Количество ячеек по горизонтали и вертикали должно быть равно количеству интервалов по обоим признакам.

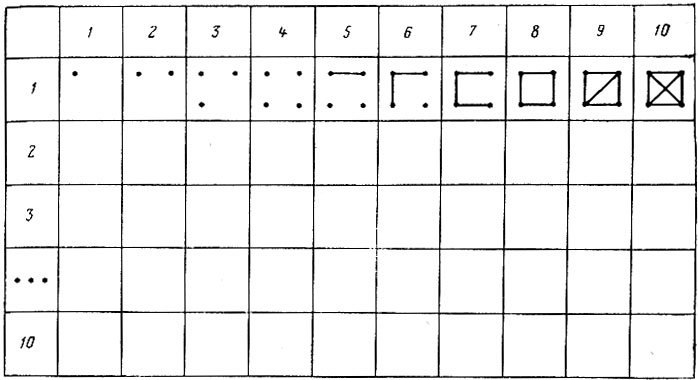
Интервалы разработочного бланка по горизонтали и вертикали в ячейках решетки обозначены порядковыми номерами от 1 до n (в рассматриваемом примере от 1 до 10). Каждую пару сочетаний в решетке отмечают точкой и линией. Если данное сочетание размерных признаков встретилось один раз, в соответствующей ячейке решетки ставят одну точку, два раза - вторую точку, четыре раза - четвертую, пять раз - между двумя любыми точками проводят линию и так до десяти. При числе сочетаний большем десяти запись снова начинают с точки в этой же ячейке.

Например, если в какой-либо ячейке решетки имеется запись это значит, что данное сочетание встретилось 27 раз. Такая запись облегчает подсчет частости распределения сочетаний, особенно при большом объеме совокупности.

Разработочный бланк, в который внесены частости распределения сочетаний двух размерных признаков, называется корреляционной решеткой.

Частости каждого горизонтального и вертикального рядов суммируют; полученные суммы записывают в графах Р_x, Р_y, обозначенных в разработочном бланке соответственно цифрами 1 и I (см. табл. III.6). При правильном расчете сумма частостей 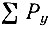должна быть равна сумме частостей 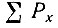и числу просмотренных карточек: 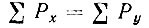(в данном примере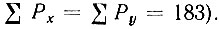

3. Выбор рабочего начала и определение параметров решетки для подсчета моментов первой и второй степени

Для установления зависимости между размерными признаками, по которым составлена корреляционная решетка, необходимо определить ряд статистических параметров: среднеарифметическую величину каждого признака М_х, М_у, среднеквадратичное отклонение σ_х, σ_у, коэффициент корреляции r и коэффициенты регрессии 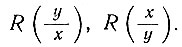Существует несколько способов определения статистических параметров. Одним из них является способ моментов, применяющийся при достаточно большом (100 и более) числе наблюдений. Моментом называется среднее из различных степеней отклонений ряда величин от какого-нибудь числа, называемого рабочим началом. Это начало выбирают по признакам x и y таким образом, чтобы вычисление было как можно более простым. Рабочим началом рекомендуется выбирать значения размерных признаков, чаще всего встречающихся в группе обследуемых людей.

В данном примере за рабочее начало для длины стопы взято А_х = Д = 238, а для ширины А_у = Ш_0,73Д = 93. Моменты а_х и а_у (графы 2 и II), соответствующие рабочему началу, по обоим признакам равны 0.

По обе стороны от рабочего начала приведены степени свободы моментов для значений размерных признаков больших и меньших, чем принятое за рабочее начало. Степени свободы записываются в вертикальных (2) и горизонтальных (II) графах разработочного бланка.

Затем определяют величины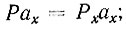

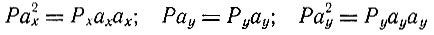
и записывают их в графы 3, 4 и III, IV. В графы 5 и V записывают результаты действий

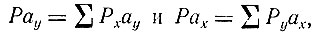
которые представляют собой сумму произведений значения каждого момента ах или ау, записанных в графе 2 и II, на сумму частостей признаков P_y и P_x, указанных в графах 1 и I.

Для удобства вычислений на узкую полоску бумаги выписывают из графы II значения степеней свободы (ряд a_y). Край полоски совмещают с ячейками каждого интервала размерного признака x (в нашем примере с ячейками интервала 222-224 для длины стопы). При этом каждое значение ау совпадает с величиной, стоящей в одной из ячеек. Значение a_y умножают на частость соответствующей ячейки и полученное произведение записывают в графу 5.

Например, для первого интервала для длины стопы Ра_у вычисляется следующим образом:

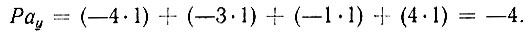
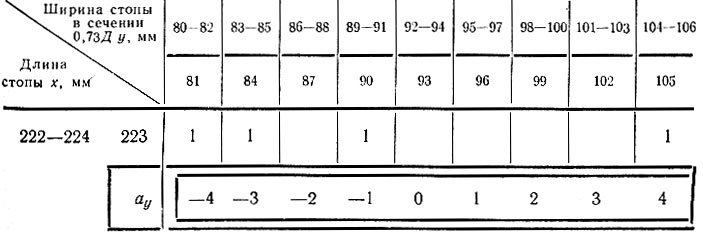
Для второго интервала по длине стопы (225-227)

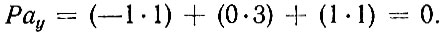
При вычислении Ра_х на полоске бумаги выписывают значения ах из графы 2, полоску совмещают с ячейками каждого интервала обхвата стопы. Так, для первого интервала Ра_х = (-5⋅1) = -5, для второго Ра_х = (-5⋅1) = -5, для третьего Ра_х = (-3⋅1) + (-2⋅1) + (-1⋅1) + (0⋅2) + (1⋅2) + (2⋅1) + (3⋅1) = 1 и т. д.

Значения Ра_ха_у в графах 6 и VI получают путем перемножения значений Ра_у (графа 5) на а_х (графа 2) и Ра_х (графа V) на а_у (графа II).

Например, для первого интервала по длине стопы Ра_ха_у = (-4)⋅(-5) = 20, для первого интервала по обхвату стопы Pa_xa_y = (-4)⋅(-5) = 20 и т. д.

Сумма Ра_xa_у интервалов по длине стопы должна быть равна сумме Ра_ха_у интервалов по обхвату стопы. В нашем примере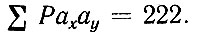

При правильном выполнении всех расчетов сумма всех значений Ра_х, записанных в графе 3 разработочного бланка, должна быть равна сумме всех значений Ра_х, записанных в графе V (для приведенного примера 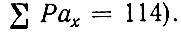Сумма всех значений Ра_у, приведенных в графе 5, должна быть равна сумме всех значений Ра_y, записанных в графе III (для приведенного примера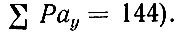

4. Определение статистических параметров

Определение среднеарифметического статистических параметров 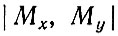производится по уравнениям:

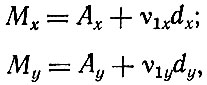
где А_х, А_у - рабочее начало;

ν_1x, ν_1у - момент первой степени;

d_x - интервал по x;

d_y - интервал по y.

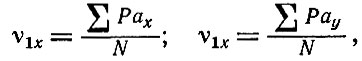
где 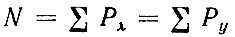- общая частость.

Определение среднеквадратичного отклонения σ производится по уравнениям:

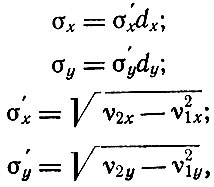
где ν_2x ν_2y - моменты второй степени;

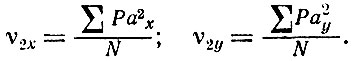
Определение коэффициента корреляции r производится по уравнениям:

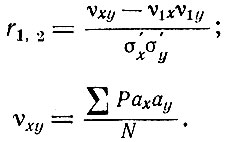
Коэффициент регрессии 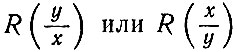служит количественной характеристикой связи между размерными признаками, т. е. показывает, как изменяется один признак при изменении другого. Величину коэффициента регрессии определяют из уравнения

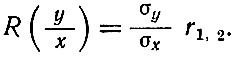
Уравнение прямой, характеризующей связь между размерными признаками, имеет вид

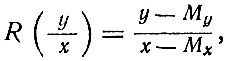
откуда

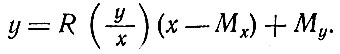
Для приведенного в разработочном бланке примера произведем подсчет всех параметров.

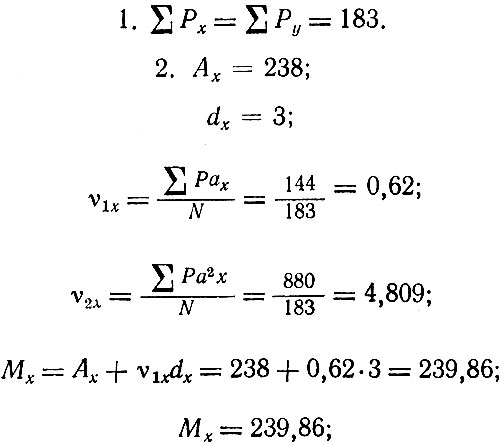
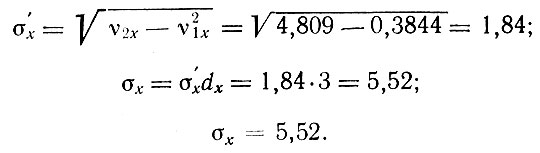
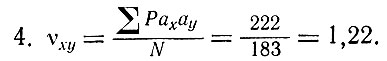
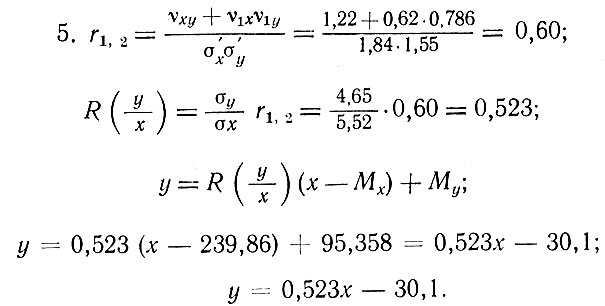
Каждому студенту выдается 100-150 карточек с одноименными размерными признаками. Для определения связи между размерными признаками нужно составить корреляционную решетку, подсчитать ее параметры и составить уравнения регрессии. Необходимо построить графики, характеризующие связь между размерными признаками, по средним значениям каждого ряда и по полученному уравнению регрессии.